|
Textbook on Computer Arithmetic, 2nd Edition
Behrooz
Parhami: 2008/08/26
|| E-mail: parhami at ece.ucsb.edu || Other
contact info at: Bottom
of this page
Go up to: B.
Parhami's teaching
and textbooks or his
home page
**** The cover design above is a placeholder. It will be
replaced with the actual cover image once the book's 2nd edition has appeared in
print ****
Parhami,
Behrooz, Computer Arithmetic: Algorithms and Hardware Designs, 2nd
edition, Oxford
University Press, New York, 2009? (ISBN TBD,
xxx + xx pp.). Available
for purchase from Oxford University Press
and various college or on-line bookstores. Instructor’s solutions manual will be
available gratis from Oxford University Press to instructors who adopt the
textbook.
Return to:
Top of this page
Preface
to the Second Edition
“In a very real sense, the writer writes in order to teach himself, to
understand himself, to satisfy himself; the publishing of his ideas, though it
brings gratifications, is a curious anticlimax.” -- Alfred Kazin
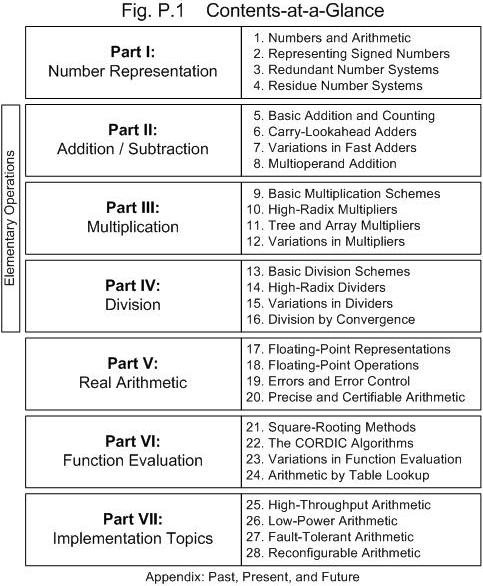
A decade has passed since the first edition
of Computer Arithmetic: Algorithms and Hardware Designs was published.
Despite continued advances in arithmetic algorithms and implementation
technologies over the past ten years, the book’s top-level design remains sound.
So, with the exception of including a new chapter on reconfigurable arithmetic,
the part/chapter structure, depicted in Fig. P.1, has been left intact in this
second edition. The new chapter replaces the previous Chapter 28, whose original
contents now appear in an appendix. The author contemplated adding a second
appendix listing websites and other Internet resources for further study. But
because Internet resource locations and contents are highly dynamic, it was
decided to include such information on the author’s companion website for the
book.
The need for a new chapter on reconfigurable
arithmetic arises from the fact that, increasingly, arithmetic functions are
being implemented on field-programmable gate arrays (FPGAs) and FPGA-like
configurable logic devices. This approach is attractive for prototyping new
designs, for producing one-of-a-kind or low-volume systems, and for use in
rapidly evolving products that need to be upgradeable in the field. It is useful
to describe designs and design strategies that have been found appropriate in
such a context. The new material blends in nicely with the other three chapters
in Part VII, all dealing with implementation topics. Examples covered in the new
Chapter 28 include table-based function evaluation, along with several designs
for adders and multipliers.
Augmentations, improvements, clarifications,
and corrections appear throughout this second edition. Material has been added
to many subsections to reflect new ideas and developments. In a number of cases,
old subsections have been merged and new subsections created for additional
ideas or designs. New end-of-chapter problems have been introduced, bringing the
total number of problems to 710 (compared with 464 in the first edition). Rather
than include new general reference sources in this preface, the author has taken
the liberty of updating and expanding the list of references at the end of the
Preface to the First Edition, so as to provide a single comprehensive list.
As always, the author welcomes
correspondence on discovered errors, subjects that need further clarification,
problem solutions, and ideas for new topics or exercises.
Behrooz Parhami (August 2008, Santa Barbara,
CA)
Return to:
Top of this page
Contents
at a Glance
Fig.
P.1. The structure of this book in
parts and chapters
(Chapter 28 is now titled "Reconfigurable Arithmetic", with the original Chapter
28 moved to an appendix; this figure will be modified shortly to reflect these changes.)
Return to:
Top of this page
Preface
to the First Edition
The context of computer arithmetic
Advances
in computer architecture over the past two decades have allowed the performance
of digital computer hardware to continue its exponential growth, despite
increasing technological difficulty in speed improvement at the circuit level.
This phenomenal rate of growth, which is expected to continue in the near
future, would not have been possible without theoretical insights, experimental
research, and tool-building efforts that have helped transform computer
architecture from an art into one of the most quantitative branches of computer
science and engineering. Better understanding of the various forms of
concurrency and the development of a reasonably efficient and user-friendly
programming model have been key enablers of this success story.
The
down side of exponentially rising processor performance is an unprecedented
increase in hardware and software complexity. The trend toward greater
complexity is not only at odds with testability and certifiability but also
hampers adaptability, performance tuning, and evaluation of the various
tradeoffs, all of which contribute to soaring development costs. A key challenge
facing current and future computer designers is to reverse this trend by
removing layer after layer of complexity, opting instead for clean, robust, and
easily certifiable designs; to devise novel methods for gaining performance and
ease-of-use benefits from simpler circuits that can be readily adapted to
application requirements.
In
the computer designers’ quest for user-friendliness, compactness, simplicity,
high performance, low cost, and low power, computer arithmetic plays a key role. It is one of oldest subfields of computer architecture. The
bulk of hardware in early digital computers resided in accumulator and other
arithmetic/logic circuits. Thus, first-generation computer designers were
motivated to simplify/share hardware to the extent possible and to carry out
detailed cost-performance analyses before proposing a design. Many of the
ingenious design methods that we use today have their roots in the bulky,
power-hungry machines of 30-50 years ago.
In
fact computer arithmetic has been so successful that it has, at times, become
transparent. Arithmetic circuits are no longer dominant in terms of complexity;
registers, memory and memory management, instruction issue logic, and pipeline
control have become the dominant consumers of chip area in today’s processors.
Correctness and high performance of arithmetic circuits is routinely expected
and episodes such as the Intel Pentium division bug are indeed rare.
The
preceding context is changing due to several factors. First, at very high clock
rates, the interfaces between arithmetic circuits and the rest of the processor
become critical. Arithmetic units can no longer be designed and verified in
isolation. Rather, an integrated design optimization is required which makes the
development even more complex and costly. Second, optimizing arithmetic circuits
to meet design goals by taking advantage of the strengths of new technologies,
and making them tolerant to the weaknesses, requires a reexamination of existing
design paradigms. Finally, Incorporation of higher-level arithmetic primitives
into hardware makes the design, optimization, and verification efforts highly
complex and interrelated.
This
is why computer arithmetic is alive and well today. Designers and researchers in
this area produce novel structures with amazing regularity. A case in point is
carry-lookahead adders. We used to think, in the not so distant past, that we
know all there is to know about carry-lookahead fast adders. Yet, new designs,
improvements, and optimizations are still appearing as of this writing. The
ANSI/IEEE standard floating-point format has removed many of the concerns with
compatibility and error control in floating-point computations, thus resulting
in new designs and products with mass-market appeal. Given the
arithmetic-intensive nature of many novel application areas (such as encryption,
error checking, and multimedia), computer arithmetic will continue to thrive for
years to come.
The
goals and structure of this book
The
field of computer arithmetic has matured to the point that a dozen or so texts
and reference books have been published. Some of these books that cover computer
arithmetic in general (as opposed to special aspects or advanced/unconventional
methods) are listed at the end of this preface. Each of these books has its
unique strengths and has contributed to the formation and fruition of the field.
The current text, Computer Arithmetic:
Algorithms and Hardware Designs, is an outgrowth of lecture notes that the
author has developed and refined over many years. Here are the most important
features of this text in comparison to the listed books:
a.
Division of material into
lecture-size chapters: In my approach to teaching, a lecture is a more or
less self-contained module with links to past lectures and pointers to what will
transpire in future. Each lecture must have a theme or title and must proceed
from motivation, to details, to conclusion. In designing the text, I have
strived to divide the material into chapters, each of which is suitable for one
lecture (1-2 hours). A short lecture can cover the first few subsections while a
longer lecture can deal with variations, peripheral ideas, or more advanced
material near the end of the chapter. To make the structure hierarchical, as
opposed to flat or linear, lectures are grouped into seven parts, each composed
of four lectures and covering one aspect of the field (Fig. P.1).
b.
Emphasis on both the underlying
theory and actual hardware designs: The ability to cope with complexity
requires both a deep knowledge of the theoretical underpinnings of computer
arithmetic and examples of designs that help us understand the theory. Such
designs also provide building blocks for synthesis as well as reference points
for cost-performance comparisons. This viewpoint is reflected, e.g., in the
detailed coverage of redundant number representations and associated arithmetic
algorithms (Chapter 3) that later lead to a better understanding of various
multiplier designs and on-line arithmetic. Another example can be found in
Chapter 22 where CORDIC algorithms are introduced from the more intuitive
geometric viewpoint.
c.
Linking computer arithmetic to
other subfields of computing: Computer arithmetic is nourished by, and in
turn nourishes, other subfields of computer architecture and technology.
Examples of such links abound. The design of carry-lookahead adders became much
more systematic once it was realized that the carry computation is a special
case of parallel prefix computation which had been extensively studied by
researchers in parallel computing. Arithmetic for/by neural networks is an area
that is still being explored. The residue number system has provided an
invaluable tool for researchers interested in complexity theory and limits of
fast arithmetic as well as to the designers of fault-tolerant systems.
d.
Wide coverage of important topics:
The current text covers virtually all important
algorithmic and hardware design topics in computer arithmetic, thus
providing a balanced and complete view of the field. Coverage of unconventional
number representation methods (Chapters 3-4), arithmetic by table-lookup
(Chapter 24), which is becoming increasingly important, multiplication and
division by constants (Chapters 9 and 13), errors and certifiable arithmetic
(Chapters 19-20), and the topics in Part VII (Chapters 25-28) do not all appear
in other textbooks.
e.
Unified and consistent
notation/terminology throughout the text: Every effort is made to use
consistent notation/terminology throughout the text. For example, r always stands for the number representation radix and s
for the remainder in division or square-rooting. While other authors have done
this in the basic parts of their texts, there is a tendency to cover more
advanced research topics by simply borrowing the notation and terminology from
the reference source. Such an approach has the advantage of making the
transition between reading the text and the original reference source easier,
but it is utterly confusing to the majority of the students who rely on the text
and do not consult the original references except, perhaps, to write a research
paper.
Summary
of topics
The
seven parts of this book, each composed of four chapters, have been written with
the following goals:
Part
I sets the stage, gives a taste of what is to come, and provides a detailed
perspective on the various ways of representing fixed-point numbers. Included
are detailed discussions of signed numbers, redundant representations, and
residue number systems.
Part
II covers addition and subtraction that form the most basic arithmetic building
blocks and are often used in implementing other arithmetic operations. Included
in the discussions are addition of a constant (counting), various methods for
designing fast adders, and multi-operand addition.
Part
III deals exclusively with multiplication, beginning with the basic shift-add
algorithms and moving on to high-radix, tree, array, bit-serial, modular, and a
variety of other multipliers. The special case of squaring is also discussed.
Part
IV covers division algorithms and their hardware implementations, beginning with
the basic shift-subtract algorithms and moving on to high-radix, pre-scaled,
modular, array, and convergence dividers.
Part V deals with real
number arithmetic, including methods for representing real numbers,
floating-point arithmetic, representation/computation errors, and methods for
high-precision and certifiable arithmetic.
Part VI covers function
evaluation, beginning with the important special case of square-rooting and
moving on to CORDIC algorithms followed by general convergence and approximation
methods, including the use of lookup tables.
Part
VII deals with broad design and implementation topics, including pipelining,
low-power arithmetic, and fault tolerance. This part concludes by providing
historical perspective and examples of arithmetic units in real computers.
Pointers
on how to use the book
For
classroom use, the topics in each chapter of this text can be covered in a
lecture of duration 1-2 hours. In his own teaching, the author has used the chapters
primarily for 1.5-hour lectures, twice a week, in a 10-week quarter, omitting or
combining some chapters to fit the material into 18-20 lectures. But the modular
structure of the text lends itself to other lecture formats, self-study, or
review of the field by practitioners. In the latter two cases, the readers can
view each chapter as a study unit (for one week, say) rather than as a lecture.
Ideally, all topics in each chapter should be covered before moving to the next
chapter. However, if fewer lecture hours are available, then some of the
subsections located at the end of chapters can be omitted or introduced only in
terms of motivations and key results.
Problems
of varying complexities, from straightforward numerical examples or exercises to
more demanding studies or mini-projects, have been supplied for each chapter.
These problems form an integral part of the book and have not been added as
afterthoughts to make the book more attractive for use as a text. A total of 464
problems are included (15-18 per chapter). Assuming that
two lectures are given per week, either weekly or biweekly homework can
be assigned, with each assignment having the specific coverage of the respective
half-part (two chapters) or full-part (four chapters) as its “title”.
An
instructor’s solutions manual is available.
The author’s detailed syllabus for the course ECE 252B at UCSB is available at:
http://www.ece.ucsb.edu/~parhami/ece_252b.htm
A simulator for numerical experimentation with various arithmetic algorithms is
available at:
http://www.ecs.umass.edu/ece/koren/arith/simulator
courtesy of Professor Israel Koren. References
to classical papers in computer arithmetic, key design ideas, and important
state-of-the-art research contributions are listed at the end of each chapter.
These references provide good starting points for doing in-depth studies or for
preparing term papers/projects. A large number of classical papers and important
contributions in computer arithmetic have been reprinted in two collections [Swar90],
[Swar09].
New
ideas in the field of computer arithmetic appear in papers presented at
bi-annual conferences, known as ARITH-n,
held in odd-numbered years [Arit]. Other conferences of interest include
Asilomar Conference on Signals, Systems, and Computers [Asil], International
Conference on Circuits and Systems [ICCS], Midwest Symposium on Circuits and
Systems [MSCS], and International Conference on Computer Design [ICCD]. Relevant
journals include IEEE Transactions on
Computers [TrCo], particularly its special issues on computer arithmetic, IEEE Transactions on Circuits and Systems [TrCS], Computers
& Mathematics with Applications [CoMa], IET Circuits, Devices &
Systems [CDS], IET Computers & Digital Techniques [CDT], IEEE Transactions on VLSI Systems [TrVL], and Journal of VLSI Signal Processing [JVSP].
Acknowledgments
The
current text, Computer Arithmetic:
Algorithms and Hardware Designs, is an outgrowth of lecture notes that the
author has used for the graduate course “ECE 252B: Computer Arithmetic” at
the University of California, Santa Barbara, and, in rudimentary forms, at
several other institutions prior to 1988. The text has benefited greatly from
keen observations, curiosity, and encouragement of my many students in these
courses. A sincere thanks to all of them!
General
references
[Arit]
International Symposium on Computer Arithmetic, Sponsored by IEEE
Computer Society. This series began with a one-day workshop in 1969 and was
subsequently held in 1972, 1975, 1978, and in odd-numbered years since 1981. The
19th symposium in the series, ARITH-19, was held on June 8-10, 2009, in
Portland, Oregon.
[Asil]
Asilomar Conference on Signals Systems, and Computes, sponsored annually
by IEEE and held on the Asilomar Conference Grounds in Pacific Grove,
California, each fall.
[Cava84]
Cavanagh, J.J.F., Digital Computer Arithmetic: Design and Implementation, McGraw-Hill,
1984.
[CDS]
IET Circuits, Devices & Systems, journal published by the Institution of
Engineering and Technology, United Kingdom.
[CDT]
IET Computers & Digital Techniques, journal published by the Institution
of Engineering and Technology, United Kingdom.
[CoMa]
Computers & Mathematics with
Applications, journal published by Pergamon Press.
[Desc06]
Deschamps, J.-P., G.J.A. Bioul, and G.D. Sutter, Synthesis of Arithmetic
Circuits: FPGA, ASIC and Embedded Systems, Wiley-Interscience, 2006.
[Erce04]
Ercegovac, M. D., and T. Lang, Digital Arithmetic, Morgan Kaufmann, 2004.
[Flor63]
Flores, I., The Logic of Computer Arithmetic, Prentice Hall, 1963.
[Gosl80]
Gosling, J.B., Design of Arithmetic Units for Digital Computers, Macmillan, 1980.
[Hwan79]
Hwang, K., Computer Arithmetic: Principles, Architecture, and Design, Wiley,
1979.
[ICCD]
International Conference on Computer Design, sponsored annually by the
IEEE Computer Society. ICCD-98 was held on October 4-7, 1998, in Austin, TX.
[ICCS]
International Conference on Circuits and Systems, sponsored annually by
the IEEE Circuits and Systems Society. The latest in this series was held on May
31 – June 3, 1998, in Monterey, CA.
[JVSP]
J. VLSI Signal Processing,
published by Kluwer Academic Publishers.
[Knut81]
Knuth, D.E., The Art of Computer Programming -- Vol. 2: Seminumerical Algorithms,
Addison-Wesley, 3rd Edition, 1997.
[Kore02] Koren, I., Computer Arithmetic Algorithms, A.K. Peters, 2nd ed., 2002.
[Kuli81]
Kulisch, U.W. and W.L. Miranker, Computer
Arithmetic in Theory and Practice, Academic Press, 1981.
[Lu04]
Lu, M., Arithmetic and Logic in Computer Systems, Wiley, 2004.
[MSCS]
Midwest Symposium on Circuits and Systems, sponsored annually by the IEEE
Circuits and Systems Society.
[Omon94]
Omondi, A.R., Computer Arithmetic Systems: Algorithms, Architecture and Implementation,
Prentice Hall, 1994.
[Rich55]
Richards, R.K., Arithmetic Operations in Digital Computers, Van Nostrand, 1955.
[Scot85]
Scott, N.R., Computer Number Systems and Arithmetic, Prentice Hall, 1985.
[Stei71]
Stein, M.L. and W.D. Munro, Introduction
to Machine Arithmetic, Addison-Wesley, 1971.
[Stin04]
Stine, J. E., Digital Computer Arithmetic Datapath Design Using Verilog HDL,
Kluwer, 2004.
[Swar90]
Swartzlander, E.E., Jr., Computer
Arithmetic, 2 Vols., IEEE Computer Society Press, 1990.
[Swar09]
Swartzlander, E. and C. Lemonds (eds.), Computer Arithmetic: A Complete
Reference, Springer, 2009 [publication info is tentative].
[TrCo]
IEEE Trans. Computers, journal
published by the IEEE Computer Society. Occasionally devotes entire special
issues or sections to computer arithmetic, e.g.: Vol. 19, No. 8, Aug. 1970; Vol.
22, No. 6, June 1973; Vol. 26, No. 7, July 1977; Vol. 32, No. 4, Apr. 1983; Vol.
39, No. 8, Aug. 1990; Vol. 41, No. 8, Aug. 1992; Vol. 43, No. 8, Aug. 1994; Vol.
47, No. 7, July 1998; Vol. 49, No. 7, July 2000; Vol. 54, No. 3, March 2005;
Vol. xx, No. xx, xxxxxx 200x.
[TrCS]
IEEE Trans. Circuits and Systems,
Parts I and II, journal published by IEEE.
[TrVL]
IEEE Trans. Very Large Scale
Integration (VLSI) Systems, journal published jointly by the IEEE Circuits
and Systems Society, Computer Society, and Solid-State Circuits Council.
[Wase82]
Waser, S. and M.J. Flynn, Introduction
to Arithmetic for Digital Systems Designers, Holt, Rinehart, & Winston,
1982.
[Wino80]
Winograd, S., Arithmetic Complexity of Computations, SIAM, 1980.
Return to:
Top of this page
Book
Reviews
The following review is for the 1st edition of the book Computer Arithmetic: Algorithms and Hardware Designs (B. Parhami,
Oxford)
Appeared
in ACM Computing Reviews, Oct. 1999
Reviewer:
Peter Turner
Computer
arithmetic (G.1.0), General (B.2.0 …), Algorithms, Design
This
well-organized text for a course in computer arithmetic at the senior
undergraduate or beginning graduate level is divided into seven parts, each
comprising four chapters. Each part is intended to occupy one or two lectures.
The book has clearly benefited from the author’s experience in teaching this
material. It achieves a nice balance among the mathematical development of
algorithms and discussion of their implementation.
Each
chapter has 15 or more exercises, of varying difficulty and nature, and its own
references. I would have liked to see a comprehensive bibliography for the whole
book as well, since this could include items that are not specifically referred
to in the text.
The
first four parts are devoted to number representation, addition and subtraction,
multiplication, and division. These are concerned with integer (or at least
fixed-point) arithmetic. The next two parts deal with real arithmetic and
function evaluation. The final part, “Implementation Topics,” covers some
practical engineering aspects.
Part
1 has chapters titled “Numbers and Arithmetic,” “Representing Signed
Numbers,” “Redundant Number Systems,” and “Residue Number Systems.”
The first begins with a brief history of the Intel division bug, which serves to
introduce the significance of computer arithmetic. A second “motivating
example” is based on high-order roots and powers. The primary content
describes fixed-radix number systems and radix conversion. It is typical of the
book that these sections contain many well-chosen examples and diagrams.
The
chapter on signed numbers covers the expected material: sign-magnitude, biased,
and complemented representations, including the use of signed digits. Redundant
number systems are introduced within the discussion of carry propagation. The
mathematical basis for carry-free addition is discussed along with its
algorithm. Residue number systems are discussed, beginning with the
representation and the choice of moduli. The explanation of conversion to and
from the binary system includes a good description of the Chinese remainder
theorem.
Part
2, on addition and subtraction, begins with the basics of half and full adders,
and carry-ripple adders. This motivates the chapter on carry-lookahead adders.
The basic idea and its implementation are presented well. This chapter finishes
with a short section on VLSI implementation, which gives pointers to further
study. Similar sections appear in most chapters. Variations on the
carry-lookahead theme are the subject of the next chapter, while Wallace and
Dadda trees of carry-save adders are the final addition topics. This provides a
natural link to multiplication.
The
basic structure of parts 3 and 4 (on multiplication and division) is the same.
There are chapters on basic and high-radix multiplication and division. Tree and
array multipliers, and special variations (for squaring and multiply-accumulate)
complete the multiplication part. The final chapter on division covers
Newton-like methods. One of my few criticisms of the book is that the
explanation of SRT and digit selection could be more extensive. A student
unfamiliar with these topics might have difficulty gaining a full understanding
of this important technique.
Part
5 is concerned with real arithmetic, and the floating-point system in
particular. The chapter on real-number representation includes a brief section
on logarithmic arithmetic, which offers the student a glimpse of alternatives.
Other schemes such as Hamada’s “Universal Representation of Real Numbers”
or symmetric level-index could also have been mentioned here. Floating-point
arithmetic is described using the integer operations. Rounding and normalization
are also discussed. Chapter 19 is a short chapter on errors and their control,
which covers most of the basics without giving all the details. For a
mathematics course on computer arithmetic, this chapter would need expanding.
The final chapter on real arithmetic describes continued fraction, multiple
precision, and interval arithmetic.
Part
6 covers function evaluation, with chapters on square-rooting, CORDIC
algorithms, variations (iterative methods and approximations), and table lookup.
Each chapter describes the basic ideas well and provides a sufficient taste of
its subject matter to point the interested student to further study. The
description of the CORDIC algorithms is more complicated than necessary. Use of
an elementary trigonometric identity would simplify some of the formulas
substantially. The use of degrees in the introduction to the CORDIC algorithm is
also a dubious choice.
The
final part has chapters on high-throughput, low-power, and fault-tolerant
arithmetic. Each is fairly brief but would serve as an introduction to some of
the practical engineering aspects of computer arithmetic.
Overall,
Parhami has done an excellent job of presenting the fundamentals of computer
arithmetic in a well-balanced, careful, and organized manner. The care taken by
the author is borne out by the almost total absence of typos or incorrect
cross-references. I would choose this book as a text for a first course in
computer arithmetic.
Return to:
Top of this page
Complete
Table of Contents
Note:
Each chapter ends with problems and references.
Part I
Number Representation
1 Numbers and Arithmetic
1.1 What is computer arithmetic?
1.2 Motivating Examples
1.3 Numbers and their encodings
1.4 Fixed-radix positional number systems
1.5 Number radix conversion
1.6 Classes of number representations
2 Representing Signed
Numbers
2.1 Signed-magnitude representation
2.2 Biased representations
2.3 Complement representations
2.4 Two's- and 1's-complement numbers
2.5 Direct and indirect signed arithmetic
2.6 Using signed positions or signed digits
3 Redundant Number Systems
3.1 Coping with the carry problem
3.2 Redundancy in computer arithmetic
3.3 Digit sets and digit-set conversions
3.4 Generalized signed-digit numbers
3.5 Carry-free addition algorithms
3.6 Conversions and support functions
4 Residue Number Systems
4.1 RNS representation and arithmetic
4.2 Choosing the RNS moduli
4.3 Encoding and decoding of numbers
4.4 Difficult RNS arithmetic operations
4.5 Redundant RNS representations
4.6 Limits of fast arithmetic in RNS
Part II
Addition/Subtraction
5 Basic Addition and Counting
5.1 Bit-serial and ripple-carry
adders
5.2 Conditions and exceptions
5.3 Analysis of carry propagation
5.4 Carry completion detection
5.5 Addition of a constant: counters
5.6 Manchester carry chains and adders
6 Carry-Lookahead Adders
6.1 Unrolling the carry recurrence
6.2 Carry-lookahead adder design
6.3 Ling adder and related designs
6.4 Carry determination as prefix computation
6.5 Alternative parallel prefix networks
6.6 VLSI implementation aspects
7 Variations in Fast
Adders
7.1 Simple carry-skip adders
7.2 Multilevel carry-skip adders
7.3 Carry-select adders
7.4 Conditional-sum adder
7.5 Hybrid designs and optimizations
7.6 Modular two-operand adders
8 Multi-Operand Addition
8.1 Using two-operand adders
8.2 Carry-save adders
8.3 Wallace and Dadda trees
8.4 Parallel counters and compressors
8.5
Adding multiple signed numbers
8.6 Modular multioperand adders
Part III
Multiplication
9 Basic Multiplication
Schemes
9.1 Shift/add multiplication
algorithms
9.2 Programmed multiplication
9.3 Basic hardware multipliers
9.4 Multiplication of signed numbers
9.5 Multiplication by constants
9.6 Preview of fast multipliers
10 High-Radix Multipliers
10.1 Radix-4 multiplication
10.2 Modified Booth's recoding
10.3 Using carry-save adders
10.4 Radix-8 and radix-16 multipliers
10.5 Multibeat multipliers
10.6 VLSI complexity issues
11 Tree and Array
Multipliers
11.1 Full-tree multipliers
11.2 Alternative reduction trees
11.3 Tree multipliers for signed numbers
11.4 Partial-tree and truncated multipliers
11.5 Array multipliers
11.6 Pipelined tree and array multipliers
12 Variations in
Multipliers
12.1 Divide-and-conquer designs
12.2 Additive multiply modules
12.3 Bit-serial multipliers
12.4 Modular multipliers
12.5 The special case of squaring
12.6 Combined multiply-add units
Part IV Division
13 Basic Division Schemes
13.1 Shift/subtract division
algorithms
13.2 Programmed division
13.3 Restoring hardware dividers
13.4 Nonrestoring and signed division
13.5 Division by constants
13.6 Radix-2 SRT division
14 High-Radix Dividers
14.1 Basics of high-radix division
14.2
Using carry-save adders
14.3
Radix-4 SRT division
14.4
General high-radix dividers
14.5
Quotient-digit selection
14.6 Using p-d plots in practice
15 Variations in
Dividers
15.1
Division with prescaling
15.2 Overlapped quotient-digit selection
15.3 Combinational and array dividers
15.4 Modular dividers and reducers
15.5 The special case of reciprocation
15.6 Combined multiply/divide units
16 Division by Convergence
16.1 General convergence methods
16.2 Division by repeated multiplications
16.3 Division by reciprocation
16.4 Speedup of convergence division
16.5 Hardware implementation
16.6 Analysis of lookup table size
Part V Real
Arithmetic
17 Floating-Point Representations
17.1 Floating-point numbers
17.2 The ANSI/IEEE floating-point standard
17.3 Basic floating-point algorithms
17.4 Conversions and exceptions
17.5 Rounding schemes
17.6 Logarithmic number systems
18 Floating-Point
Operations
18.1 Floating-point adders/subtractors
18.2 Pre- and postshifting
18.3
Rounding and exceptions
18.4
Floating-point multipliers and dividers
18.5 Fused-multiply-add units
18.6 Logarithmic arithmetic unit
19 Arithmetic Errors and
Error Control
19.1 Sources of computational errors
19.2 Invalidated laws of algebra
19.3 Worst-case error accumulation
19.4. Error distribution and expected errors
19.5 Forward error analysis
19.6 Backward error analysis
20 Precise and Certifiable Arithmetic
20.1 High precision and
certifiability
20.2 Exact arithmetic
20.3 Multiprecision arithmetic
20.4 Variable-precision arithmetic
20.5 Error bounding via interval arithmetic
20.6 Adaptive and lazy arithmetic
Part VI
Function Evaluation
21 Square-Rooting Methods
21.1 The pencil-and-paper algorithm
21.2 Restoring shift/subtract algorithm
21.3 Binary non-restoring algorithm
21.4 High-radix square-rooting
21.5 Square-rooting by convergence
21.6 Fast hardware square-rooters
22 The CORDIC Algorithms
22.1 Rotations and
pseudorotations
22.2 Basic CORDIC iterations
22.3 CORDIC hardware
22.4 Generalized CORDIC
22.5 Using the CORDIC method
22.6 An algebraic formulation
23 Variations in Function
Evaluation
23.1 Additive/multiplicative
normalization
23.2 Computing logarithms
23.3 Exponentiation
23.4 Division and square-rooting, again
23.5 Use of approximating functions
23.6 Merged arithmetic
24 Arithmetic by Table
Lookup
24.1 Direct and indirect table lookup
24.2 Binary-to-unary reduction
24.3 Tables in bit-serial arithmetic
24.4 Interpolating memory
24.5
Piecewise lookup tables
24.6 Multipartite table methods
Part VII
Implementation Topics
25 High-Throughput Arithmetic
25.1 Pipelining of arithmetic
functions
25.2 Clock rate and throughput
25.3 The Earle latch
25.4 Parallel and digit-serial pipelines
25.5 On-line or digit-pipelined arithmetic
25.6 Systolic arithmetic units
26 Low-Power Arithmetic
26.1 The need for low-power design
26.2 Sources of power consumption
26.3 Reduction of power waste
26.4 Reduction of activity
26.5 Transformations and trade-offs
26.6 New and emerging methods
27 Fault-Tolerant Arithmetic
27.1 Faults, errors, and error codes
27.2 Arithmetic error-detecting codes
27.3 Arithmetic error-correcting codes
27.4 Self-checking function units
27.5 Algorithm-based fault tolerance
27.6 Fault-tolerant RNS arithmetic
28 Reconfigurable Arithmetic
28.1 Programmable logic devices
28.2 Adder designs for FPGAs
28.3
Multiplier designs for FPGAs
28.4 Tabular and distributed arithmetic
28.5 Function evaluation on FPGAs
28.6 Beyond fine-grained devices
Appendix Past, Present,
and Future
A.1 Historical perspective
A.2 Early high-performance machines
A.3 Deeply pipelined vector machines
A.4 The DSP revolution
A.5 Supercomputers on our laps
A.6 Trends, outlook, and resources
Index
Return to:
Top of this page
From
the Preface to the Instructor’s Solution Manual
**** The intro to this section will be
updated for the 2nd edition ****
The book’s Web page, given below, also
contains an errata and a host of other material:
http://www.ece.ucsb.edu/~parhami/text_comp_arit.htm
The author would appreciate the reporting of
any error in the textbook or in this manual, suggestions for additional
problems, alternate solutions to solved problems, solutions to other problems,
and sharing of teaching experiences. Please e-mail your comments to
parhami@ece.ucsb.edu
or send them by regular mail to the
author’s postal address:
Department of Electrical and Computer Engineering
University of California
Santa Barbara, CA 93106-9560, USA
Contributions
will be acknowledged to the extent possible.
Return to:
Top of this page
Presentations
The following PowerPoint and PDF presentations for the seven parts of the
text are available for downloading (file sizes 0.8 to 1.2 MB):
-
Presentation
for Part I: Number Representation (ppt,
pdf, last updated 2008/04/07)
-
Presentation
for Part II: Addition / Subtraction (ppt,
pdf, last updated 2008/04/15)
-
Presentation
for Part III: Multiplication (ppt,
pdf, last
updated 2008/04/30)
-
Presentation
for Part IV: Division (ppt,
pdf, last
updated 2008/05/19)
-
Presentation
for Part V: Real Arithmetic (ppt,
pdf, last updated 2008/05/28)
-
Presentation
for Part VI: Function Evaluation (ppt,
pdf, last updated 2008/05/30)
-
Presentation
for Part VII: Implementation Topics (ppt, pdf, last updated 2007/12/07)
Return to:
Top of this page
Errors in the 2nd Edition
None at this time.
For a list of errors in, and additions to,
the 1st edition, see the website for Parhami's
Computer Arithmetic, 1st ed.
Return to:
Top of this page
Additional Material and Resources
None at this time.
Return to:
Top of this page || Go up to: B.
Parhami's teaching
and textbooks or his
home page
|
