StochDynTools

Status: Work in progress. The documentation is fairly complete, but this software is still in its earlier stages of development and perhaps not very user friendly. Please email me if you have questions/problems using it. I’ll be happy to help.
          
Requires the symbolic toolbox and all tests were done with MATLAB R2007a (it is unclear if it works with older versions of MATLAB)

Download: [tar file]

This set of MATLAB scripts provides a set of functions that compute approximate moment dynamics for a stochastic network of chemical reactions. This approximation is based on the moment closure techniques described in the following references:

Joćo Hespanha, Abhyudai Singh. Stochastic Models for Chemically Reacting Systems Using Polynomial Stochastic Hybrid Systems. Int. J. on Robust Control, Special Issue on Control at Small Scales: Issue 1, 15(15):669—689, Sep. 2005.

Abhyudai Singh, Joćo Hespanha. LogNormal Moment Closures for Biochemical Reactions. In Proc. of the 45th Conf. on Decision and Contr., Dec. 2006.

A typical set of chemical reactions is specified by a .net file of the following form:

% Filename: enzyme_with_Et_St.che

% Michaelis-Menten kinetics, keeping track of one fast variable (free enzyme)

% and three slow variables (total subtrate, total enzymes, product)

species:

        E  stochastic    2;  % free enzyme                       (fast variable)

        Et deterministic 3;  % total enzymes = free + compound   (slow variable)

 

        St stochastic   11;  % total substrate = free + compound (slow variable)

        P  stochastic    2;  % product                           (slow variable)

 

parameters:

        K_C =  1;              % rate constant for  S + E -> ES

        D_C = 20;              % rate constant for  ES -> S + E

        K_P =.05;              % rate constant for  ES -> P + E

 

reactions:

        % fast reversible reaction

        rate = K_C*(St-Et+E)*E;  {E} > {E-1};               % S + E -> ES

        rate = D_C*(Et-E);       {E} > {E+1};               % ES -> S + E

 

        % slow product reaction

        rate = K_P*(Et-E);       {St,P,E} > {St-1,P+1,E+1}; % ES -> P + E

% END of .net file

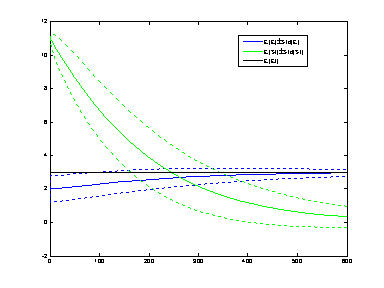
The following commands produce the evolution of the moment dynamics shown in the figure below

net=readNet('enzyme_with_Et_St.net');

[mdyn2,x20,texrules]=closureDynamics(net,2,'derMatch','fun');

Tmax=600;                      % maximum simulation time

[t,mu]=ode23s(@(t,x)fun(x),[0,Tmax],x20);

h=plotCMoments(net,mdyn2,t,mu,'E','b-','St','g-','Et','k-'); legend(h(1:3:end),'E[E]\pm{}Std[E]','E[St]\pm{}Std[St]','E[Et]','location','best');

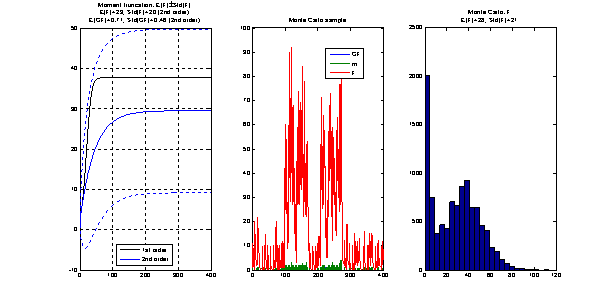
The following picture is taken from an example included in the package and compares the moments dynamics obtained by truncation with Monte Carlo simulations from Petzold’s StochKit.

 

Bibliographic citation

When used in research, please acknowledge the use of this software with the following reference:

Joćo Hespanha. StochDynTools — a MATLAB toolbox to compute moment dynamics for stochastic networks of bio-chemical reactions. Available at http://www.ece.ucsb.edu/~hespanha, May. 2007.

or if you use latex/bibtex:

@Misc{HespanhaDec06,

  key =     {matlab,c,biology},

  author =  {Joćo Pedro Hespanha},

  title =   {\texttt{StochDynTools} --- a {MATLAB} toolbox to

                  compute moment dynamics for stochastic networks of

                  bio-chemical reactions},

  howpublished = {Available at \url{http://www.ece.ucsb.edu/~hespanha}},

  month =  may,

  year =   2007

}

Disclaimer

This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU General Public License for more details (http://www.gnu.org/copyleft/gpl.html)